Epistasis and the inference problem
Biological research today
is defined by the low cost of sequencing data.
This makes studies that attempt to explain biological variation by sequencing many individuals that vary
for a trait and then model that trait as a function of the genotypes easy to
perform.
Unfortunately, these studies usually fail to provide useful information. The ability to predict a trait from sequence data is often either poor (e.g. for height) or the predictions are good but no biologically useful insights can be obtained from the model structure. The reason for this is that inference with these studies is fundamentally a large P and small N problem. Millions of genetic markers can be sequenced, but comparatively few individuals are available for sequencing. Worse, due to shared population history and linkage the genetic markers in these studies are often heavily aliased.
Progress is therefore typically only made in limited studies where the trait distinctly varies between diverged populations or ethical breeding is possible. This suggests we may be stuck spending more money to sequence more individuals or spending more time in the lab to generate better data. However, it could also be possible that we are simply missing out on a big opportunity to gain greater insights because we are using an inference model that does not match the biological reality for these traits.
The fundamental question about any proposed statistical model is how it expects the genes underlie a trait to interact with each other. The typical inference model used for these studies is the classic linear model. As virtually all studies lack enough degrees of freedoms to simultaneously infer all main effects, much less higher level interactions, epistasis between genetic markers, detected as significant higher order effects, is usually either ignored or occasionally checked for with a heuristic method based on the effect hierarchy principle or more principled stochastic methods and these approaches can be very inefficient.
The question then is whether or not a more realistic understanding of epistasis might allow for more parsiomonious models with better predictions and causative genetic markers. In earlier work I had shown that in general epistatic interactions of loci within a protein are highly nonlinear. However, since most proteins are segregated as a single unit on the chromosome this rather difficult complication is essentially alleviated by the data structure. More interestingly, in recent work I have shown that epistatic interactions between proteins is expected to follow a general trend of diminishing returns epistasis. Markers segregating in many human association study are most likely to exhibit this form of epistasis, and so I asked:
Given a consistent pattern of diminishing returns epistasis, how well do current statistical models perform and can they be improved?
To get at this question, we first boil down diminishing returns epistasis to its simplest possible form, which really just a statement that, in general, for a given change in the genetic effect of an allele x, the phenotypic effect, P, is inversely proportional to its current value. That is, an allele which would make an otherwise short person much taller will have almost no effect on a person who is already quite tall. Functions that exhibit this behavior are log and power functions, and examples of such functions are shown below for various values of the epistatic parameter n.
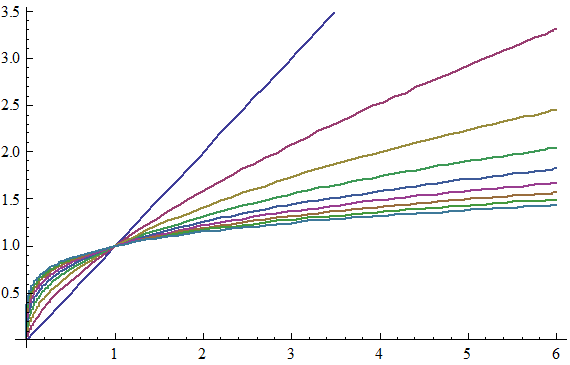
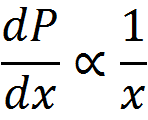
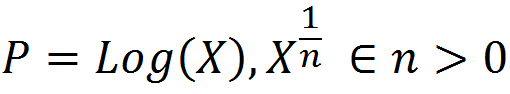
This simple model gives us a map from summed genetic effects (the x-axis) to phenotypic effects (the y-axis) and we can use this framework to investigate the results of model misspecification. It is clear from the diagram above that the linear model is most likely to fail when the standing genetic variation sits on the "crest" of the curve as here the effect is large for low values but very small for high values, and although monotonically increasing, this conflicting information likely diminishes our ability to properly infer allelic effects when past work suggests they should exist.
After selecting the area of genotype/phenotype space most likely to be problematic, we than simulate biological data from a generative model that has allelic distributions similar to those found in nature and plausible allelic effect sizes for a neutral trait not under selection to give us a "worst case" evaluation of the canonical model. This is schematically shown below. Graphs in the top rows represent the simulation of genotypes and allelic effects, these determine the summed genetic (x) value which is mapped to a phenotypic value by the relevant function. Histograms of the genotypic values, phenotypic values and a plot of them shown against each other are displayed in the lower half of the panel.
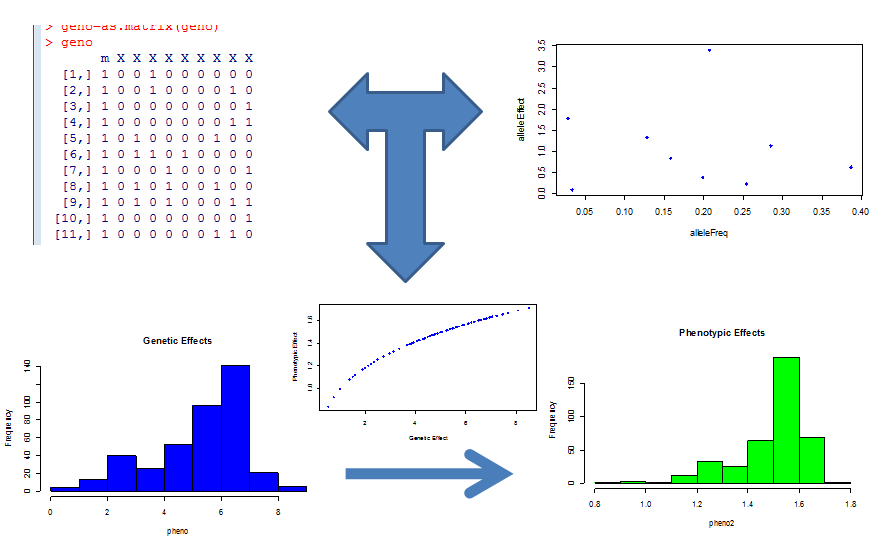
We can then analyze this data with standard methods and compare them to the simulated reality. So what did this tell us? Intuitively, we knew that as the number of genes that underlie a phenotype gets larger, the central limit theorem would kick in and the linear model would be a great approximation. But this of course is the large P small N domain where we already knew we were out of luck, and we were interested in the smaller P relatively larger N domain. That is, phenotypes for which the number of underlying genetic factors was too large for simple mendelian studies to pick up, but still small enough where we could perhaps tease them out if we had a correct model. This range roughly corresponds to ~7-20 genetic variants underlying a trait.
What I found is that, surprisingly, the convergence to the asymptotics is remarkably fast, even with very few genetic factors underlying a trait. The results could be shown here, but they are essentially identical to what one gets when they have a moderate dataset that properly fits the model if given a simple log transformation; the residual plots indicate obvious model misspecification and the data will never fit exactly, but the qualitative behavior is there and the imporant genetic factors can be identified clearly. In fact, simply simulataneously fitting a simple box-cox transformation during analysis always recovers the correct model.
The important conclusions from this are:
- Association studies are unlikely to be impaired by the patterns of epistasis most likely influencing the traits under study (diminishing returns epistasis).
- For empirically observed and biologically relevant parameters, this pattern of epistasis means that one should attempt a power transformation after they have selected a genetic model to improve fit and accuracy. The exact usefulness of this transformation will depend on the particulars of the study and genetic structures, but in general it is not expected to add that much. By analogy, the analysis without the transform is like filling ones plate at the buffet counter and then finding out that by using a transformation one can maybe get a side-soup or at least a cracker for a soup they may have already picked up. This is significant from a computational perspective since it means a simultaneous search for the transformation parameter and model variables need not be performed, greatly reducing the dimensionality of the problem.
Additionally we have the conclusion that many a statistician has come to after thinking long and hard about a problem, which is that R.A. Fisher was right! Although his geometric model (weren't they all?) has fueled a half century of epistasis research, Fisher never cared much about epistasis because he always thought that any issues it created could be solved by a simple transformation of the data. Granted, he wasn't totally correct on this. This depends on an allele having the same qualitative effect when introduced on any genetic background (so good is always good, even if how good depends on the background). My own research has shown this is often not true within proteins and even if it is true this can have major effects on evolving populations. However, for the case where we are inferring effects from existing genetic variation, this almost certainly holds and we can proceed as he did.